Berdasarkan persamaan kontinuaitas, laju aliran fluida dapat berubah-ubah sepanjang jalur fluida. Tekanan juga dapat berubah-ubah tergantung pada ketinggian seperti pada keadaan statis dan juga tergantung pada laju aliran. Kita bisa mendapatkan hubungan penting yang disebut persamaan Bernoulli yang menghubungkan tekanan, laju aliran dan ketinggian untuk aliran, fluida inkompresibel yang ideal.
Persamaan Bernoulli merupakan persamaan penting untuk menganalisis sistem perpipahan, stasiun pembangkit listrik tenaga air, dan penerbangan pesawat.
Persamaan Bernoulli merupakan persamaan penting untuk menganalisis sistem perpipahan, stasiun pembangkit listrik tenaga air, dan penerbangan pesawat.
Ketergantungan tekanan pada laju mengikuti persamaan kontinuitas. Ketika fluida inkompresibel mengalir sepanjang tabung alir dengan penampang yang berubah-ubah, lajunya pasti berubah dan karena itu elemen dari fluida memiliki percepatan. Jika tabung horisontal, gaya yang menyebabkan percepatan ini digunakan oleh fluida di sekelilingnya. Ini berarti bahwa tekanan pasti berbeda pada penampang melintang yang berbeda. Jika tekanannya sama di setiap tempat, gaya total pada setiap elemen fluida akan berharga nol. Ketika tabung alir horisontal menyempit dan laju elemen fluida meningkat, fluida akan bergerak menuju daerah bertekanan rendah untuk mendapatkan gaya ke depan total untuk mempercepatnya. Jika ketinggian juga berubah, peningkatan perbedaan tekanan akan terjadi.
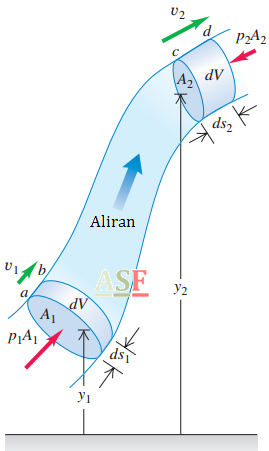
Untuk menurunkan persamaan Bernoulli, kita teorema usaha-energi pada fluida dalam daerah tabung alir. Dalam gambar 1 kita perhatikan elemen fluida pada keadaan mula-mula terletak di antara dua penampang a dan c. Laju pada ujung yang rendah dan ujung yang lebih tinggi masing-masing adalah v1 dan v2. Dalam selang waktu yang singkat dt fluida yang awalnya berada pada a bergerak ke b sejauh ds1 = v1dt, dan fluida yang mula-mula di c bergerak ke d sejauh ds2 = v2dt. Luas penampang melintang pada kedua ujung adalah A1 dan A2, seperti pada gambar. Fluida adalah inkompresibel, karena itu dengan persamaan kontinuitas volume fluida dV yang melalui setiap penampang nelintang sepanjang waktu dt adalah sama, yaitu dV = A1ds1 = A2ds2.
Kita akan mengitung usaha (kerja) yang dilakukan pada elemen fluida selama dt. Tekanan pada kedua ujung adalah p1dan p2; gaya pada penampang di a adalah p1A1dan gaya pada c adalah p2A2. Usaha total, dW yang dilakukan pada elemen oleh fluida disekelilingnya selama perpindahan ini adalah
dW = p1A1ds1 – p2A2ds2 = (p1– p2)dV (1)
suku kedua memiliki tanda negatif karena gaya pada c berlawanan dengan arah perpindahan fluida.
Usaha, dW adalah akibat gaya-gaya selain gaya konservatif gravitasi, sehingga besarnya sama dengan perubahan energi mekanik total (energi kinetik ditambah energi potensial gravitasi) yang berasosiasi dengan elemen fluida. Energi mekanik untuk elemen fluida antara penampang b dan c tidak berubah. Pada awal dt fluida antara a dan b memiliki volume A1ds1, massa ρA1ds1dan energi kinetik ½ m1v12 = ½ ρ(A1ds1)v12. Pada ujung dt, fluida di antara c dan d memiliki energi kinetik sebesar ½ m2v22= ½ ρ(A2ds2)v22. Perubahan total energi kinetik dEk selama waktu dt adalah
dEk = ½ ρ.dV(v22 – v12) (2)
bagaimana dengan perubahan energi potensial gravitasi???
Pada awal dt, energi potensial untuk massa antara a dan b adalah dm gy1 = ρ dV gy1. Pada akhir dt, energi potensial untuk massa antara c dan d adalah dm gy2 = dm dV gy2. Perubahan energi potensial total dEp sepanjang dt adalah
dEp = ρ dV g(y2 – y1) (3)
dengan menggabungkan persamaan (1), (2) dan (3) dalam persamaan energi dW = dEk + dEp, kita peroleh
(p1 – p2)dV = ½ ρ.dV(v22– v22) + ρ dV g(y2 – y1)
p1 – p2 = ½ ρ(v22 – v12) + ρg(y2 – y1) (4)
persamaan (4) adalah persamaan Bernoulli (Bernoulli’s equation), yang menyatakan bahwa usaha atau kerja yang dilakukan pada satu satuan volume fluida oleh fluida di sekitarnya adalah sama dengan jumlah perubahan energi kinetik dan energi potensial tiap satuan volume yang terjadi selama aliran. Kita juga dapat menginterpretasikan persamaan (4) dalam fungsi tekana. Suku pertama pada bagian kanan adalah selisih tekanan yang diasosiasikan dengan perubahan laju fluida. Suku kedua pada bagian kanan adalah penambahan perbedaan tekanan yang disebabkan oleh berat fluida dan perbedaan ketinggian kedua ujung.
Kita dapat menuliskan kembali persamaan (4) dalam bentuk yang lebih meyakinkan sebagai berikut,
p1 + ½ ρ v12 + ρgy1 = p2 + ½ ρv22 + ρgy2 (Persamaan Bernoulli) (5)
indeks 1 dan 2 mengacu pada sebarang titik sepanjang tabung aliran, sehingga kita juga dapat menulis,
p + ½ ρv2 + ρgy = konstan (6)
CATATAN: Ketika fluida tidak bergerak (sehingga v1 = v2 = 0), persamaan (5) berubah menjadi hubungan tekanan pada fluida statis.
PERHATIAN: Kita tekankan kembali bahwa persamaan Bernoulli hanya berlaku bagi fluida inkompesibel, aliran fluida tunak tanpa gesekan. Itu adalah persamaan sederhana yang mudah untuk digunakan.
0 comments:
Post a Comment